Machine Learning
#
다음 사이트등을 참조하여 머신 러닝 관련 자료 정리.
Machine Learning 분류
#
머신 러닝은 지도학습, 비지도학습, 강화학습으로 분류. 지도학습은 다시 회귀와 분류, 비지도 학습은 군집화,변환,연관으로 분류
Supervised Learning
Regression
Classification
Unsupervised Learning
Clustering
Transform
Association
Reinforcement Learning
Linear Regression#
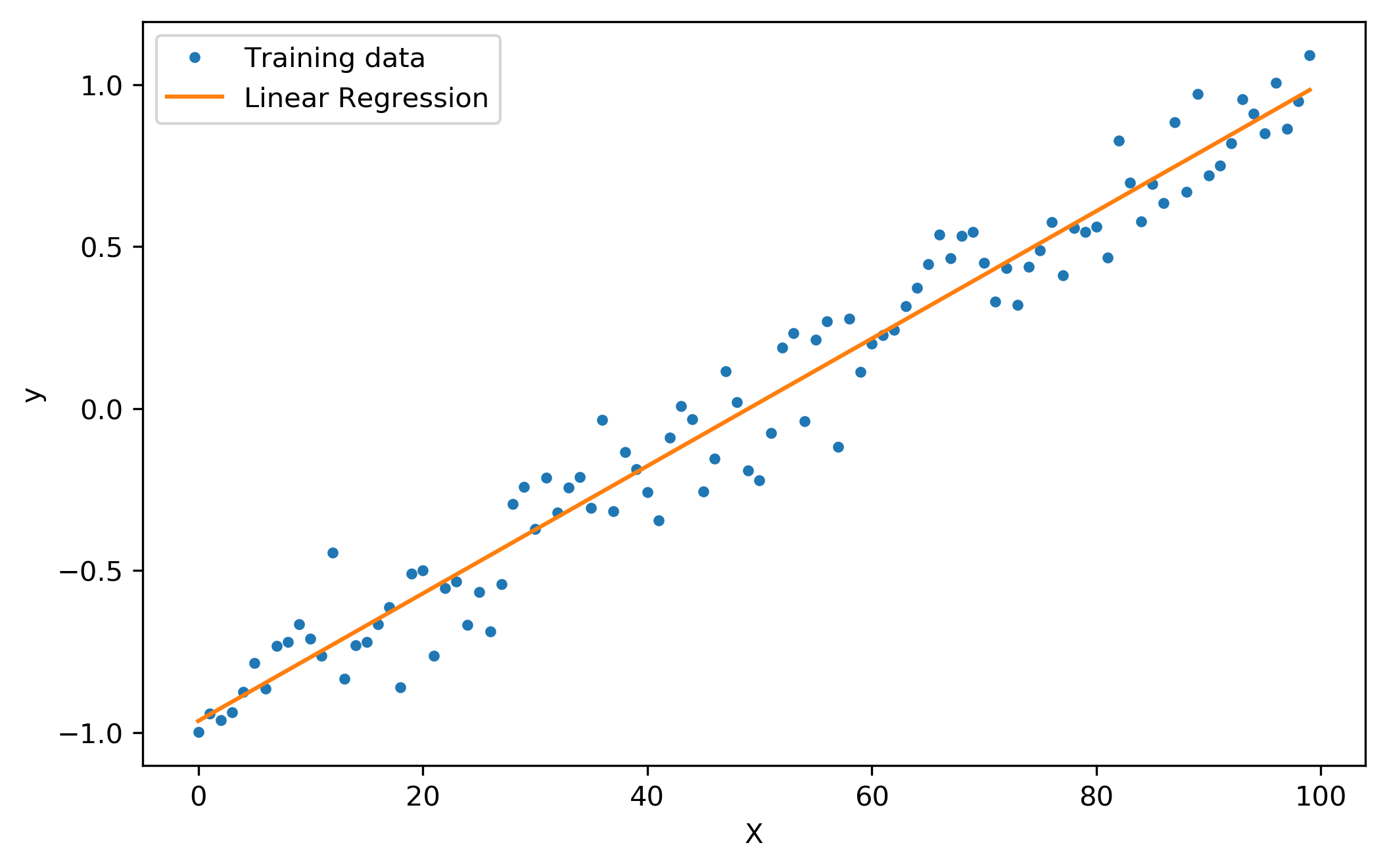
Regression이란 전체의 평균으로 회귀하려는 속성을 나타냄. 데이터의 분포를 가장 잘 설명 할 수 있는 직선의 방정식을 찾아내는 것을 의미.
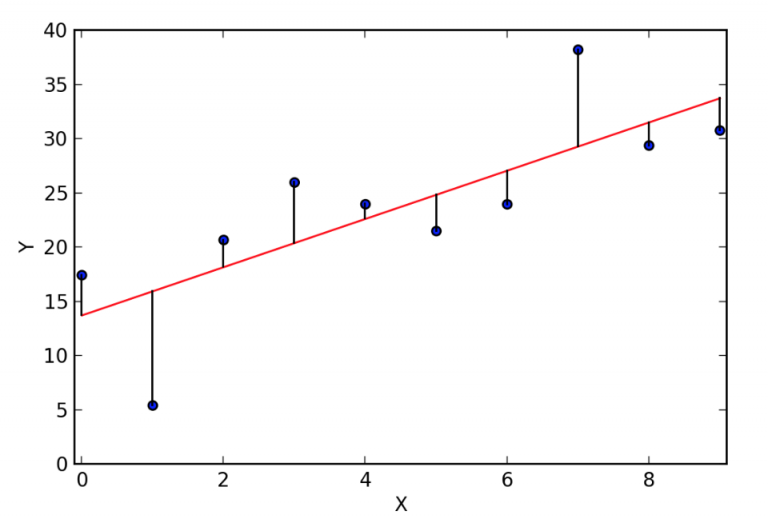
Cost는 데이터와 직선 차이의 합. 음수, 양수 모두 존재함으로 제곱을 사용.
Goal은 가설과 실제 데이터 차이의 제곱이 최소가 되는 기울기와 절편은 찾는 문제.
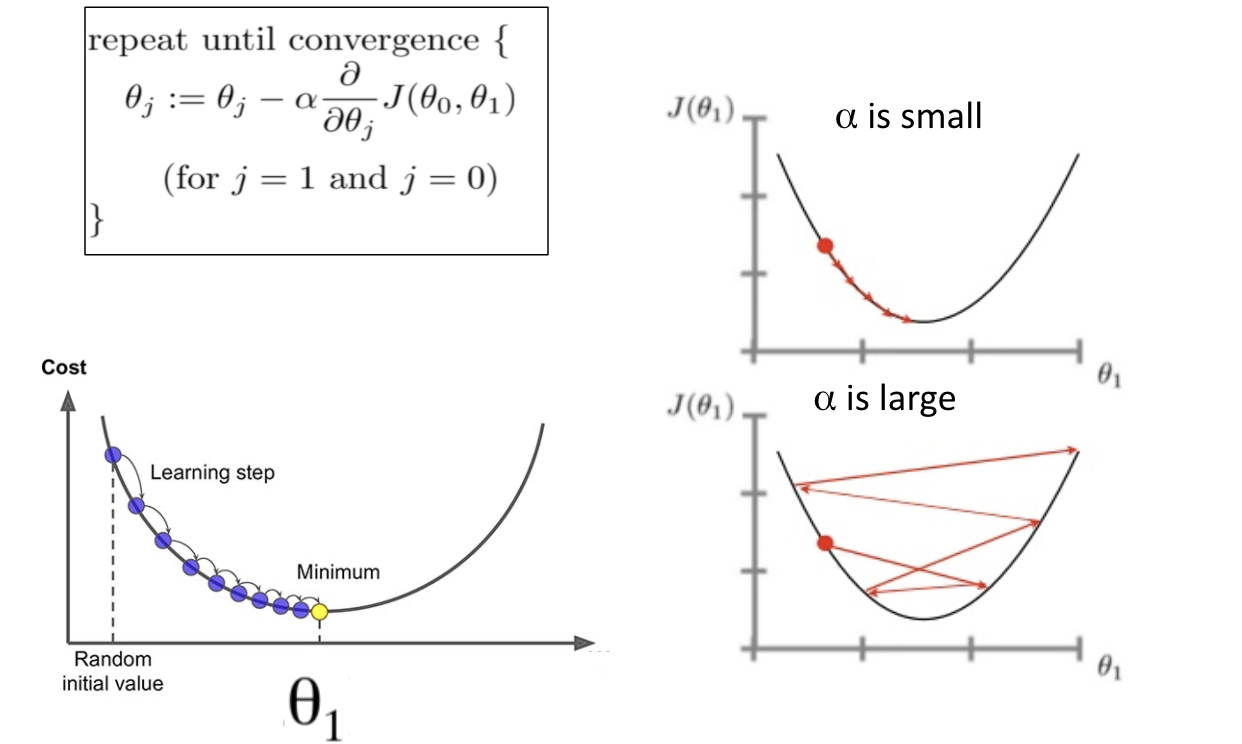
Gradient Descent
#
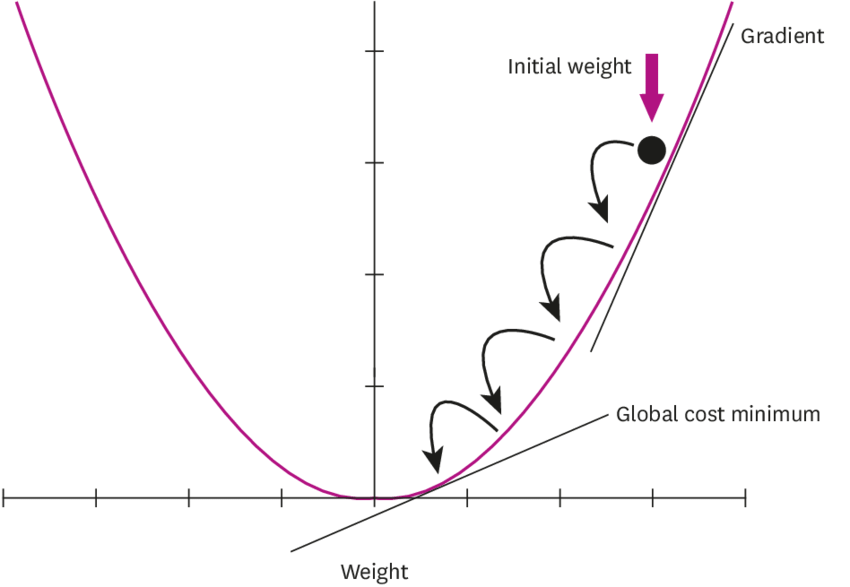
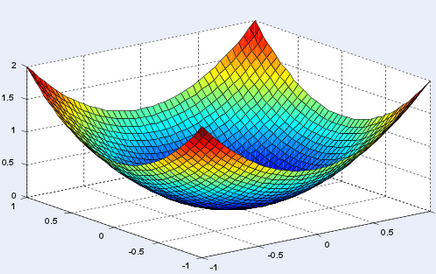
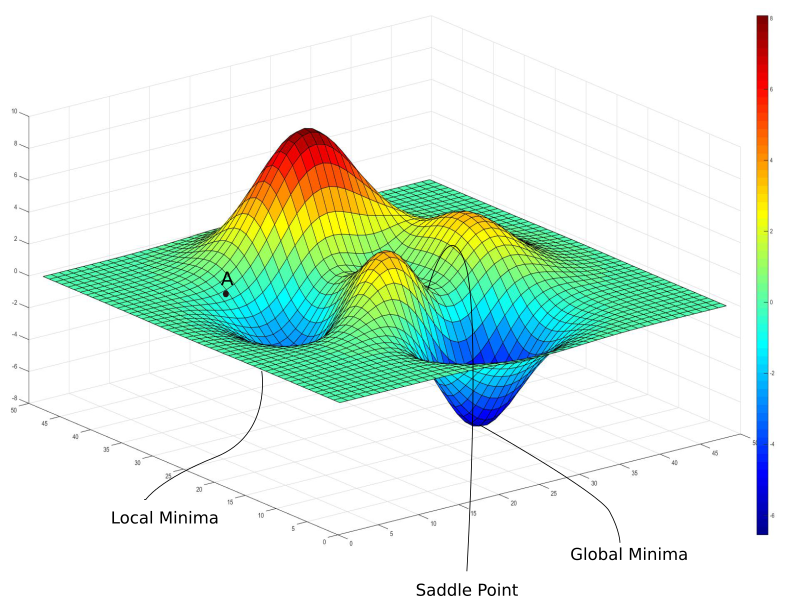
임의 점에서 시작 학습률 만큼 기울기가 낮은 쪽으로 진행하며 최적해를 탐색하는 방식을 경사하강법이라 함. Convext 상황에서는 잘 작동하나 Local Optimal이 존재할 경우 문제가 발생됨
Derivative
#
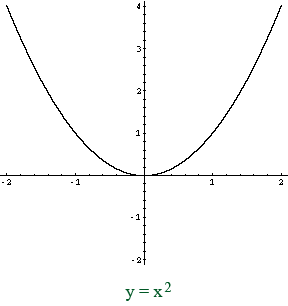
함수 f(x)에 대한 미분은 아래와 같음. x의 변화량이 0으로 수렴할때 y의 변화량을 의미.
미분 기초 정리
미분의 의미
즉 x = 2 일때 미분 f(x)는 4의 변화를 가지게 됨
즉 x = 1 일때 미분 f(x)는 2의 변화를 가지게 됨
즉 x = 0 일때 미분 f(x)는 0의 변화를 가지게 됨
즉 x의 한점에서 y의 변화량을 통해 위의 x^2이 Cost라 가정하고 반복한다면 기울기가 0이되는 즉 Cost가 최저인 점을 구할 수 있음.
입력변수가 하나 이상인 다변수 함수에서 사용하는 편미분을 사용. 편미분은 미분하고자 하는 변수를 제외하고 나머지는 상수로 취급.
복합 함수를 위해 Chain Rule을 통해 미분. 특정 함수를 치환하여 약분 개념을 적용. 두 함수 곱의 미분은 단순 곱이 아니며 Product Rule이 적용됨.
Loss Function
#
다시 선형회귀에서 실측되는 데이터와 f(x) = wx+b간 error는 최소가 되어야함. Error가 최소가 되는 W,B를 연속적으로 측정하기 위해 사용되는 것이 손실함수임.
원 기울기에서 학습률*미분만큼을 감소시키며 기울기가 0이 되는 최적해로 진행됨.
여기서 학습률은 최적해를 향한 진행 폭을 결정. 작을 경우 성능이 저하. 클 경우 학습이 진행되지 않음.
이론적으로 Convex Function이라면 대체로 최적해를 잘 찾을 수 있으나 그렇지 않다면 Parameter에 따라 결과가 상이할 수 있음.
Dot Product
#
모든 요소들의 행렬곱을 통해 계산.
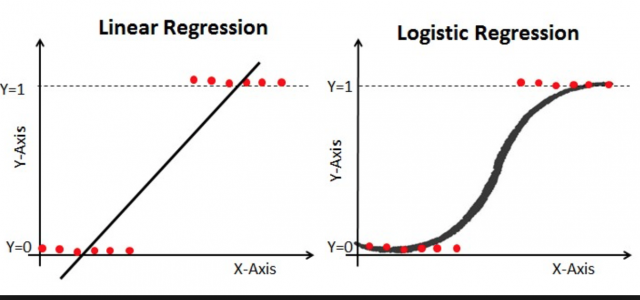
Logistic Regression
#
Regression을 통해 처리된 결과를 Classification 처리함. Linear Regression의 결과는 수치형 값을 가지게 됨으로 분류 문제에 취약. Linear한 결과를 Logistic Regression을 통해 선택의 결과로 대치.
분류의 문제를 위해 지수 함수
\( e^x \)
를
\( e^{-x} \)
로 전환 후
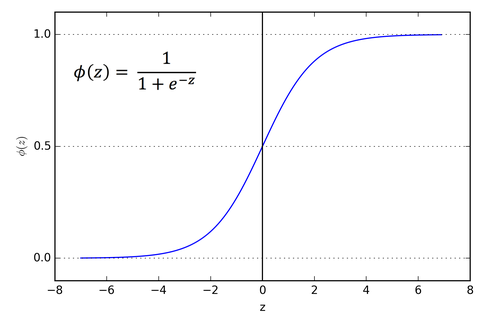
\( \frac{1}{1 + e^{-x}} \)
에 대입하여 x의 좌측으로 진행할수로
\( \infty \)
에 가까워지며 0에 수렴하게되고 x의 우측으로 진행하게 될수록 0에 수렴하면서 1에 가까워지는 결과가 됨.
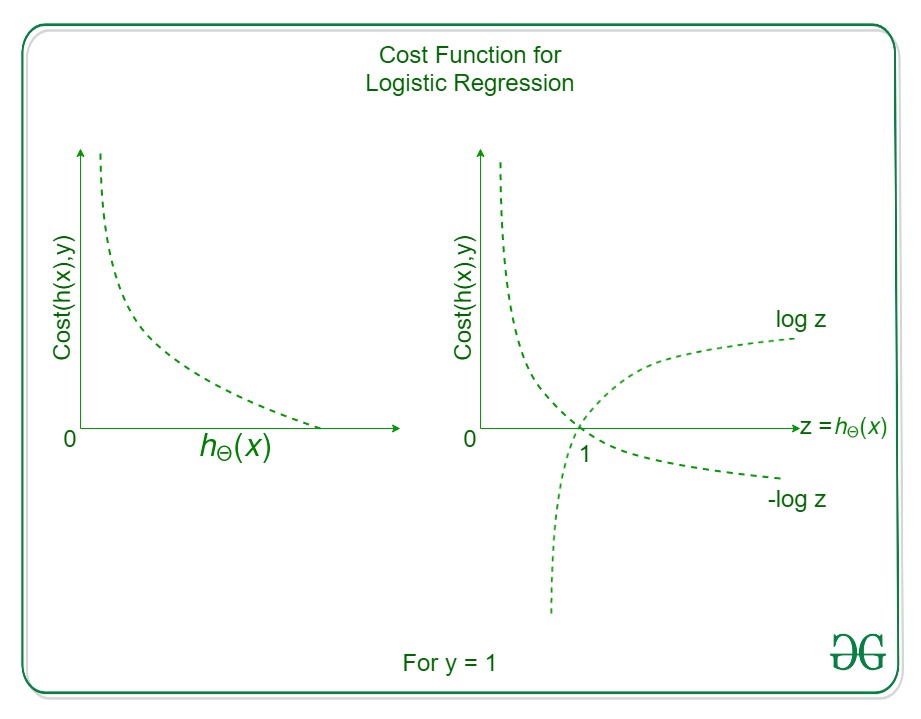
Logistic Regression의 Cost Function은 y = 1 일때와 y = 0 일때로 구분할 수 있는데 y = 1 일때는
\( \log(h(x)) \)
의 역
\( -\log(h(x)) \)
을 취해 0으로 근접할 수록 오차가
\( \infty \)
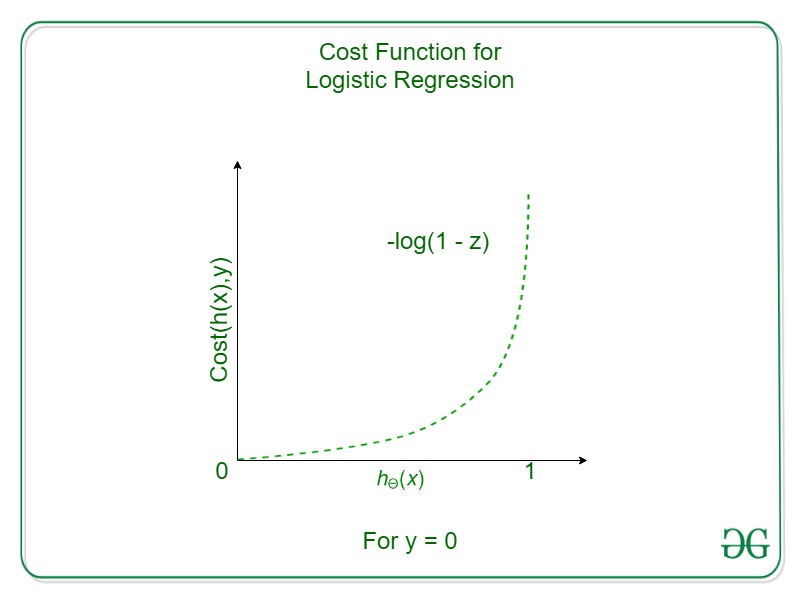
에 수렴하게 됨. 반대로 y = 0 일때는
\( \log(1 - h(x)) \)
와 같이 1에서 차감하여 1에 근접할 수록 오차가
\( \infty \)
에 수렴하함. 이 두 식을 합하면 Logistic Regression의 Convex한 Cost Funtion이 되게 됨.
Cross-Entropy 유도의 또다른 설명은 다음과 같음.
하나의 입력 x에 대해 출력이 1일 확률을 y로 정의. y는 0 또는 1일임으로 y = sigmoid(Wx+b)로 나타낼 수 있음. 입력 x에 대해 출력이 0일 확률은 1이 나타날 확률의 나머지임으로 1-y 임. 확률 변수 C는 0 또는 1 이외에는 존재하지 않음으로 베르누이 시행을 전제로 하며 베르누이 분포의 확률질량함수(PMF)는 아래와 같이 정의됨. 이를 Log 변환을 통해 Convex의 형태와 극점의 위치를 유지하며 곱을 선형의 조합 꼴로 풀 수 있도록 변환함.
Bayes Theorem
#
Logit, Sigmoid, Softmax를 유도하기 위해 다음과 같은 확률의 개념이 선행되어야함.
불확실성 하의 의사 결정의 문제를 수학적으로 다룰때 사용되는 베이즈의 정리(Bayes Theorem)와 전확률 법칙(law of total probability)는 다음과 같음.
표본 공간 S를 n개로 나누었을때 사건 A의 확률은 다음과 같이 나타나며 총합은 1이됨.
일반적으로
\( A_1,A_2,A_3 \)
가 서로 Mutually Exclusive이고 이들의 합집합이 표본공간과 S와 같으면 사건
\( A_1,A_2,A_3 \)
는 표본공간 S의 분할이라고 정의. 특정 사건 B가 나타날 확률은 전확률 공식에 의거 다음과 같이 표현할 수 있음.
\(P(A_1)\)
,
\(P(A_2)\)
,
\(P(A_3)\)
은 미리 알고 있다는 의미로 사전확률(Prior Probability)로 불리고,
\(P(B|A_1)\)
,
\(P(B|A_2)\)
,
\(P(B|A_3)\)
는 우도(Likelihood Probability)라 부름.
\( P(A_1|B) \)
는 사건 B를 관측한 후 원인이 되는 사건 A의 확률을 따졌다는 의미에서 사후확률(Posterior Probability)로 정의되며 다음과 같이 나타낼 수 있음.
practice 2 : 딸기맛 문제
...
사탕주머니 1 : 딸기맛 30개, 포도맛 10
사탕주머니 2 : 딸기맛 20개, 포도맛 20
두 주머니에서 임의로 골랐을때 딸기였다면 주머니1에서 나왔을 확률은?
\( P(H) \)
: 사전확률 -> 주머니1을 고를 확률
\( P(D|H) \)
: 우도 -> 주머니1의 딸기 확률
\( P(D) \)
: 한정상수 -> 딸기를 고를 확률
\( P(H|D)) \)
: 사후확률 -> 주머니1에서 딸기를 골랐을 확률
\( P(H|D)) = \frac {P(H)P(D|H)}{P(D)} = \frac { \frac {1}{2} * \frac {3}{4} }{ \frac {5}{8} } = \frac {3}{5} \)
이때 한정상수
\( P(D) \)
는 상호배제(Mutually Exclusive)와 전체포괄(Collectively Exhaustive)의 원칙에서 같은 값을 지니며 계산이 생략됨
Point
Theory1
Theory2
사전확률 P(H)
1/2
1/2
우도P(D
H)
3/4
사전확률*우도
3/8
1/4
한정상수P(D)
5/8
5/8
사후확률P(H
D)
3/5
\( P(H|D) = \frac {P(H)P(D|H)}{P(D)} = \frac { \frac {1}{2} * \frac {3}{4} }{ \frac {5}{8} } = \frac {3}{5} \)
Logit / Sigmoid / Softmax
#
Logit /Sigmoid /Softmax의 관계를 정리
Logit은 Log Odds를 의미.
이를 Log를 이용해 0~1의 범위로 한정된 Logit을 도출
여기서 Softmax는 Sigmoid를 K개 이상으로 일반화 하여 유도.
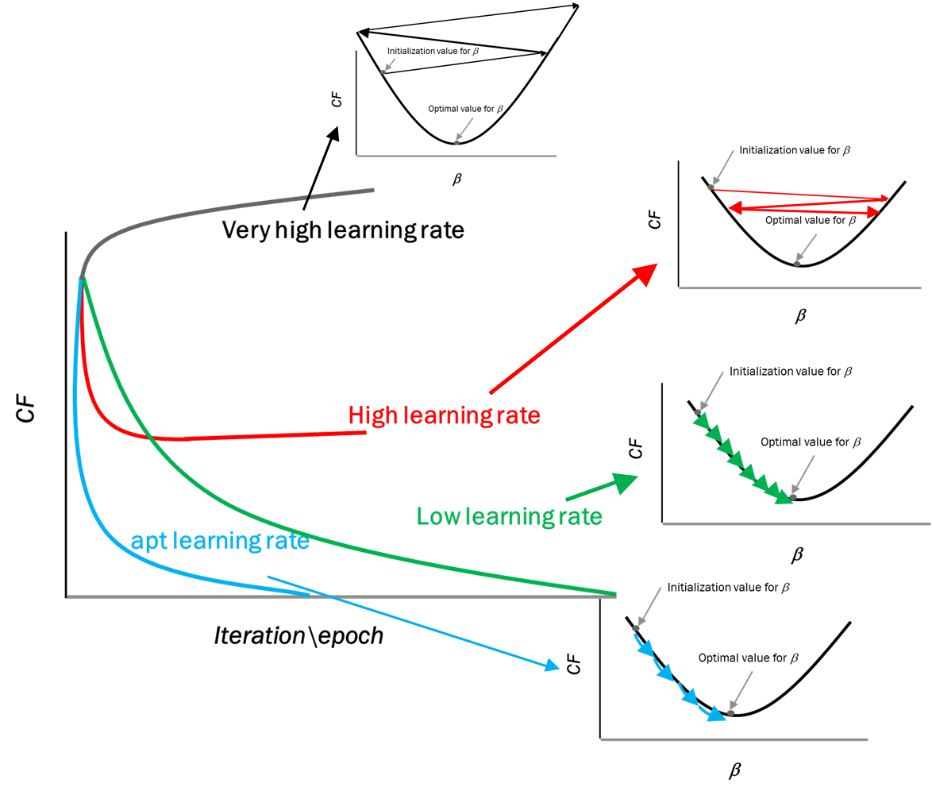
Learning Rate
#
Learning Rate와 학습의 상관관계는 아래와 같음. Learning rate가 너무 높을 경우 Overshooting이 발생되며 너무 작을 경우 학습이 매우 더디게 진행됨.
학습시점에 따라 Learning rate를 조정하는 decay방식이 있음.
Step deacy : N epoch or validation loss
Exponential decay :
\( \alpha = \apha 0 \epsilon - kt \)
1/t decay :
\( \alpha = \apha 0 (1+kt) \)
inverse time decay
natural exponential decay
piecewise constant
polynomical decay
Data Preprocessing
#
Data의 분포가 편중되어 있을 경우 표준화(Standardization)와 정규화(Normalization)을 통해서 전처리.
Feature Scaling
Standardization :
\( x_{new} = \frac {x - \mu}{\sigma} \)
Normalization :
\( x_{new} = \frac {x - x_{min}}{x_{max} - - x_{min}} \)
Noisy Data
학습에 필요한 Data로 정제하는 전처리 과정.
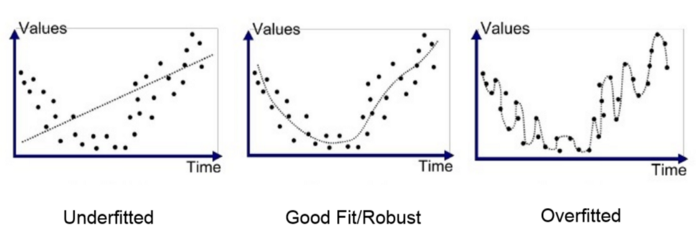
Overfitting
#
Underfitting : High bias 상태. 학습이 덜된 상태.
Overfitting : High variance. 학습이 너무되어 주어진 data에만 맞춰진 상태.
Solution
Set features : Get more training data
Set features : Smaller set of features (PCA)
Set features : Add additional features (for underfitting)
Regularization (Add term to loss)
Linear regression with regularization
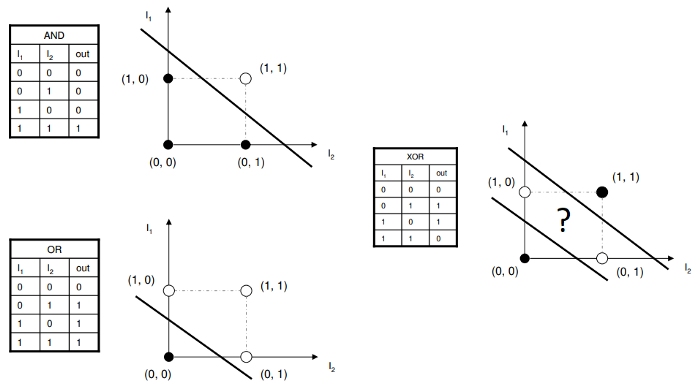
XOR Prolem
#
1958년 Frank Rosenblatt에 의에 제안된 신경망 시스템의 모델로 McGullock, Pitts, Hebb의 연구를 기초로 하고 있음.
하지만 XOR의 문제는 Linear Regression으로 해결할 수 없다는 수학적 결론을 내림. (Perceptrons by Marvin Minsky)
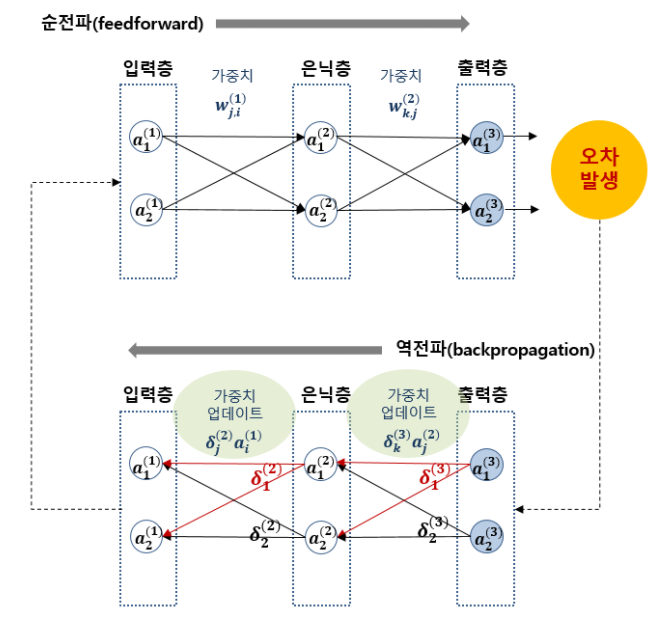
Backpropagation
#
1974, 1982 Paul Werbos, 1986 Hinton에 의해 정립된 개념. 순전파에서 목표값과 모델의 계산값의 오차를 구한후 그 오차값을 역방향으로 전파하며 노드들의 변수들을 갱신하는 알고리즘. 다만 복잡한 Neural Networks 환경에서는 역전파되는 값들이 소실되는 Vanishing Gradient 현상이 발생됨. 2006년 2007년 Hinton과 Bengio에 의해 초기 Parameter에 의한 영향이 주목되며 Deep Learning이라는 용어가 등장함.
Geoffrey Hinton’s summary
Our labeled datasets were thousands of times too small.
Our computers were millions of times too slow.
We initialized the wieghts in a stupid way.
We used the wrong type of non-linearity.
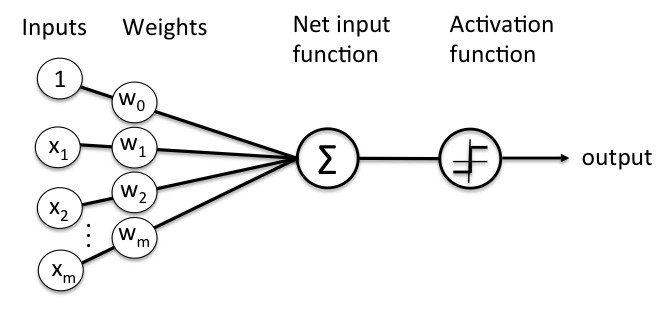
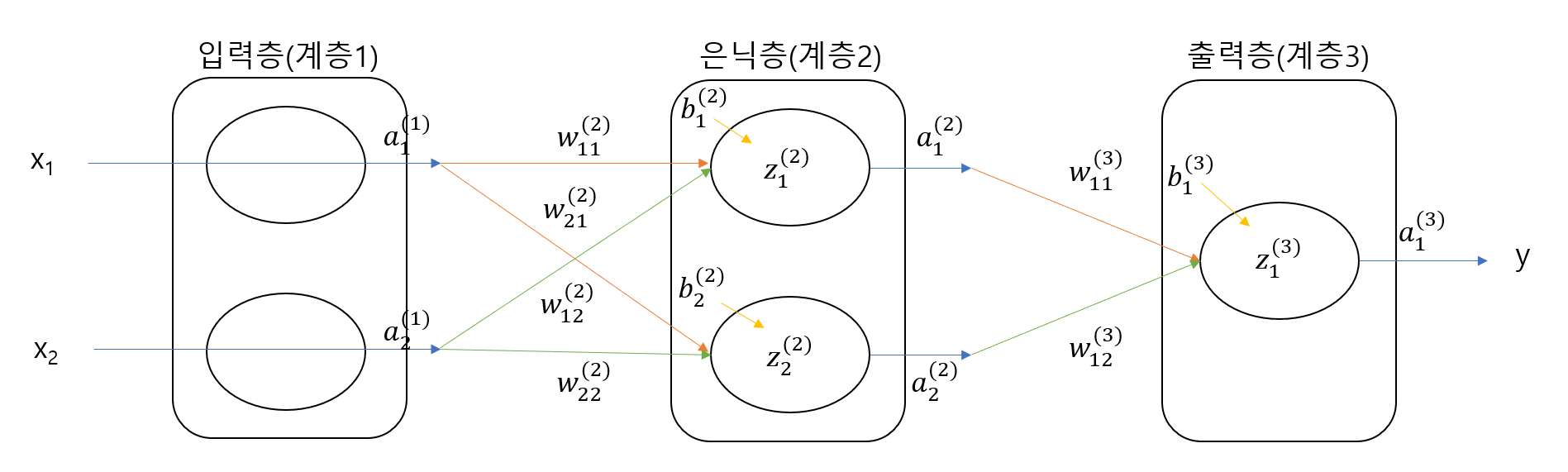
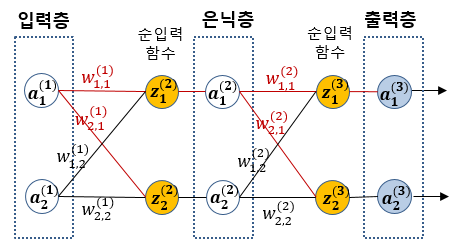
Node Notation
Backpropagation
Chain Rule을 이용한 국소 미분된 오차 역전파
Sigmoid 미분
preparation of backpropagation
...
입력층 선형회귀값 (z)
* 없음
입력층 출력값 (a)
\( a_{1}^{(1)} = x_{1} \)
\( a_{2}^{(1)} = x_{2} \)
은닉층 선형회귀값 (z)
\( z_{1}^{(2)} = a_{1}^{(1)} w_{1,1}^{(2)} + a_{2}^{(1)} w_{1,2}^{(2)} + b_{1}^{(2)} \)
\( z_{2}^{(2)} = a_{1}^{(1)} w_{2,1}^{(2)} + a_{2}^{(1)} w_{2,2}^{(2)} + b_{2}^{(2)} \)
은닉층 출력값 (a)
\( a_{1}^{(2)} = sigmoidz(z_{1}{(2)} \)
\( a_{2}^{(2)} = sigmoidz(z_{2}{(2)} \)
출력층 선형회귀값 (z)
\( z_{1}^{(3)} = a_{1}^{(2)} w_{1,1}^{(3)} + a_{2}^{(2)} w_{1,2}^{(3)} + b_{1}^{(3)} \)
\( z_{2}^{(3)} = a_{1}^{(2)} w_{2,1}^{(3)} + a_{2}^{(2)} w_{2,2}^{(3)} + b_{2}^{(3)} \)
출력층 출력값 (a)
\( a_{1}^{(3)} = sigmoidz(z_{1}{(3)} \)
\( a_{2}^{(3)} = sigmoidz(z_{2}{(3)} \)
\( E = \frac {1}{n} \displaystyle\sum_{i=1}^{n}(t_{i}^{(3)} - a_{i}^{(3)})^2 = \frac {1}{2} ( (t_{1}^{(3)} - a_{1}^{(3)})^2 + (t_{2}^{(3)} - a_{2}^{(3)})^2 ) \)
\( E_1 + E_2 = \frac {1}{2} (t_{1}^{(3)}-a_{1}^{(3)})^2 + \frac {1}{2} (t_{2}^{(3)}-a_{2}^{(3)})^2 \)
\( W^{(2)} = \begin{pmatrix} w_{(1,1)}^{(2)} & w_{(2,1)}^{(2)} \\ w_{(1,2)}^{(2)} & w_{(2,2)}^{(2)} \end{pmatrix} , W^{(3)} = \begin{pmatrix} w_{(1,1)}^{(3)} & w_{(2,1)}^{(3)} \\ w_{(1,2)}^{(3)} & w_{(2,2)}^{(3)} \end{pmatrix} \)
\( W^{(2)} = W^{(2)} - \alpha \frac {\partial E}{\partial W^{(2)}} \to \frac {\partial E}{\partial W^{(2)}} = \frac {\partial E}{\partial W_{(1,1)}^{(2)}} , \frac {\partial E}{\partial W_{(2,1)}^{(2)}} , \frac {\partial E}{\partial W_{(1,2)}^{(2)}} , \frac {\partial E}{\partial W_{(2,2)}^{(2)}} \)
\( W^{(3)} = W^{(3)} - \alpha \frac {\partial E}{\partial W^{(3)}} \to \frac {\partial E}{\partial W^{(3)}} = \frac {\partial E}{\partial W_{(1,1)}^{(3)}} , \frac {\partial E}{\partial W_{(2,1)}^{(2)}} , \frac {\partial E}{\partial W_{(1,2)}^{(3)}} , \frac {\partial E}{\partial W_{(2,2)}^{(3)}} \)
\( b^{(2)} = \begin{pmatrix} b_{(1)}^{(2)} & b_{(2)}^{(2)} \end{pmatrix} , b^{(3)} = \begin{pmatrix} b_{(1)}^{(3)} & b_{(2)}^{(3)} \end{pmatrix} \)
\( b^{(2)} = b^{(2)} - \alpha \frac {\partial E}{\partial b^{(2)}} \to \frac {\partial E}{\partial b^{(2)}} = \frac {\partial E}{\partial b_{(1)}^{(2)}} , \frac {\partial E}{\partial b_{(2)}^{(2)}} \)
\( b^{(3)} = b^{(3)} - \alpha \frac {\partial E}{\partial b^{(3)}} \to \frac {\partial E}{\partial b^{(3)}} = \frac {\partial E}{\partial b_{(1)}^{(3)}} , \frac {\partial E}{\partial b_{(2)}^{(3)}} \)
output layer 1
...
\(
\frac {\partial E} {\partial W_{(1,1)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial W_{(1,1)}^{(3)}} + \frac {\partial E_{(2)}} {\partial W_{(1,1)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial a_{(1)}^{(3)}} * \frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} * \frac {\partial z_{(1)}^{(3)}}{\partial w_{(1,1)}^{(3)}} \)
\(
= \frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(1)}^{(3)} - a_{(1)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(1)}^{(3)}} * \frac { \partial sigmoid (z_{(1)}^{(3)}) } { \partial z_{(1)}^{(3)} } * \frac { \partial ( a_{(1)}^{(2)} w_{(1,1)}^{(3)} + a_{(2)}^{(2)} w_{(1,2)}^{(3)} + b_{(1)}^{(3)} ) } { \partial w_{(1,1)}^{(3)} } \)
\(
\frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(1)}^{(3)} - a_{(1)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(1)}^{(3)}}
= \frac{1}{2} \cdotp \frac {\partial (t_{(1)}^{(3)})^2 + (a_{(1)}^{(3)})^2 -2 t_{(1)}^{(3)} a_{(1)}^{(3)} } { \partial a_{(1)}^{(3)} }\)
\(
\space \space \space \space = \frac{1}{2} \cdotp (0 + 2*(a_{(1)}^{(3)})^{(2-1)} + -2 t_{(1)}^{(3)}) = a_{(1)}^{(3)} - t_{(1)}^{(3)}\)
\(
\frac { \partial sigmoid (z_{(1)}^{(3)}) } { \partial z_{(1)}^{(3)} } =
sigmoid(z_{(1)}^{(3)}) * (1-sigmoid(z_{(1)}^{(3)}))\)
\(
\frac { \partial ( a_{(1)}^{(2)} w_{(1,1)}^{(3)} + a_{(2)}^{(2)} w_{(1,2)}^{(3)} + b_{(1)}^{(3)} ) } { \partial w_{(1,1)}^{(3)} }
= a_{(1)}^{(2)} + 0 + 0\)
\(
= (a_{(1)}^{(3)} - t_{(1)}^{(3)}) * sigmoid(z_{(1)}^{(3)}) * (1-sigmoid(z_{(1)}^{(3)})) * a_{(1)}^{(2)}\)
\(
sigmoid(z_{(1)}^{(3)}) = a_{(1)}^{(3)}\)
\(
= (a_{(1)}^{(3)} - t_{(1)}^{(3)}) * a_{(1)}^{(3)} * ( 1 - a_{(1)}^{(3)} ) * a_{(1)}^{(2)}\)
\(
\frac {\partial E} {\partial W_{(2,1)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial W_{(2,1)}^{(3)}} + \frac {\partial E_{(2)}} {\partial W_{(2,1)}^{(3)}}
= \frac {\partial E_{(2)}} {\partial a_{(2)}^{(3)}} * \frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} * \frac {\partial z_{(2)}^{(3)}}{\partial w_{(2,1)}^{(3)}} \)
\(
= \frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(2)}^{(3)} - a_{(2)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(2)}^{(3)}} * \frac { \partial sigmoid (z_{(2)}^{(3)}) } { \partial z_{(2)}^{(3)} } * \frac { \partial ( a_{(1)}^{(2)} w_{(2,1)}^{(3)} + a_{(2)}^{(2)} w_{(2,2)}^{(3)} + b_{(2)}^{(3)} ) } { \partial w_{(2,1)}^{(3)} } \)
\(
\frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(2)}^{(3)} - a_{(2)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(2)}^{(3)}}
= \frac{1}{2} \cdotp \frac {\partial (t_{(2)}^{(3)})^2 + (a_{(2)}^{(3)})^2 -2 t_{(2)}^{(3)} a_{(2)}^{(3)} } { \partial a_{(2)}^{(3)} }\)
\(
\space \space \space \space = \frac{1}{2} \cdotp (0 + 2*(a_{(2)}^{(3)})^{(2-1)} + -2 t_{(2)}^{(3)}) = a_{(2)}^{(3)} - t_{(2)}^{(3)}\)
\(
\frac { \partial sigmoid (z_{(2)}^{(3)}) } { \partial z_{(2)}^{(3)} } =
sigmoid(z_{(2)}^{(3)}) * (1-sigmoid(z_{(2)}^{(3)}))\)
\(
\frac { \partial ( a_{(1)}^{(2)} w_{(2,1)}^{(3)} + a_{(2)}^{(2)} w_{(2,2)}^{(3)} + b_{(2)}^{(3)} ) } { \partial w_{(2,1)}^{(3)} }
= a_{(1)}^{(2)} + 0 + 0\)
\(
= (a_{(2)}^{(3)} - t_{(2)}^{(3)}) * sigmoid(z_{(2)}^{(3)}) * (1-sigmoid(z_{(2)}^{(3)})) * a_{(1)}^{(2)}\)
\(
sigmoid(z_{(2)}^{(3)}) = a_{(2)}^{(3)}\)
\(
= (a_{(2)}^{(3)} - t_{(2)}^{(3)}) * a_{(2)}^{(3)} * ( 1 - a_{(2)}^{(3)} ) * a_{(1)}^{(2)}\)
\(
\frac {\partial E} {\partial W_{(1,2)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial W_{(1,2)}^{(3)}} + \frac {\partial E_{(2)}} {\partial W_{(1,2)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial a_{(1)}^{(3)}} * \frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} * \frac {\partial z_{(1)}^{(3)}}{\partial w_{(1,2)}^{(3)}} \)
\(
= \frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(1)}^{(3)} - a_{(1)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(1)}^{(3)}} * \frac { \partial sigmoid (z_{(1)}^{(3)}) } { \partial z_{(1)}^{(3)} } * \frac { \partial ( a_{(1)}^{(2)} w_{(1,1)}^{(3)} + a_{(2)}^{(2)} w_{(1,2)}^{(3)} + b_{(1)}^{(3)} ) } { \partial w_{(1,2)}^{(3)} } \)
\(
\frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(1)}^{(3)} - a_{(1)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(1)}^{(3)}}
= \frac{1}{2} \cdotp \frac {\partial (t_{(1)}^{(3)})^2 + (a_{(1)}^{(3)})^2 -2 t_{(1)}^{(3)} a_{(1)}^{(3)} } { \partial a_{(1)}^{(3)} }\)
\(
\space \space \space \space = \frac{1}{2} \cdotp (0 + 2*(a_{(1)}^{(3)})^{(2-1)} + -2 t_{(1)}^{(3)}) = a_{(1)}^{(3)} - t_{(1)}^{(3)}\)
\(
\frac { \partial sigmoid (z_{(1)}^{(3)}) } { \partial z_{(1)}^{(3)} } =
sigmoid(z_{(1)}^{(3)}) * (1-sigmoid(z_{(1)}^{(3)}))\)
\(
\frac { \partial ( a_{(1)}^{(2)} w_{(1,1)}^{(3)} + a_{(2)}^{(2)} w_{(1,2)}^{(3)} + b_{(1)}^{(3)} ) } { \partial w_{(1,2)}^{(3)} }
= a_{(1)}^{(2)} + 0 + 0\)
\(
= (a_{(1)}^{(3)} - t_{(1)}^{(3)}) * sigmoid(z_{(1)}^{(3)}) * (1-sigmoid(z_{(1)}^{(3)})) * a_{(2)}^{(2)}\)
\(
sigmoid(z_{(1)}^{(3)}) = a_{(1)}^{(3)}\)
\(
= (a_{(1)}^{(3)} - t_{(1)}^{(3)}) * a_{(1)}^{(3)} * ( 1 - a_{(1)}^{(3)} ) * a_{(2)}^{(2)}\)
\(
\frac {\partial E} {\partial W_{(2,2)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial W_{(2,2)}^{(3)}} + \frac {\partial E_{(2)}} {\partial W_{(2,2)}^{(3)}}
= \frac {\partial E_{(2)}} {\partial a_{(2)}^{(3)}} * \frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} * \frac {\partial z_{(2)}^{(3)}}{\partial w_{(2,2)}^{(3)}} \)
\(
= \frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(2)}^{(3)} - a_{(2)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(2)}^{(3)}} * \frac { \partial sigmoid (z_{(2)}^{(3)}) } { \partial z_{(2)}^{(3)} } * \frac { \partial ( a_{(1)}^{(2)} w_{(2,1)}^{(3)} + a_{(2)}^{(2)} w_{(2,2)}^{(3)} + b_{(2)}^{(3)} ) } { \partial w_{(2,2)}^{(3)} } \)
\(
\frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(2)}^{(3)} - a_{(2)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(2)}^{(3)}}
= \frac{1}{2} \cdotp \frac {\partial (t_{(2)}^{(3)})^2 + (a_{(2)}^{(3)})^2 -2 t_{(2)}^{(3)} a_{(2)}^{(3)} } { \partial a_{(2)}^{(3)} }\)
\(
\space \space \space \space = \frac{1}{2} \cdotp (0 + 2*(a_{(2)}^{(3)})^{(2-1)} + -2 t_{(2)}^{(3)}) = a_{(2)}^{(3)} - t_{(2)}^{(3)}\)
\(
\frac { \partial sigmoid (z_{(2)}^{(3)}) } { \partial z_{(2)}^{(3)} } =
sigmoid(z_{(2)}^{(3)}) * (1-sigmoid(z_{(2)}^{(3)}))\)
\(
\frac { \partial ( a_{(1)}^{(2)} w_{(2,1)}^{(3)} + a_{(2)}^{(2)} w_{(2,2)}^{(3)} + b_{(2)}^{(3)} ) } { \partial w_{(2,2)}^{(3)} }
= a_{(2)}^{(2)} + 0 + 0\)
\(
= (a_{(2)}^{(3)} - t_{(2)}^{(3)}) * sigmoid(z_{(2)}^{(3)}) * (1-sigmoid(z_{(2)}^{(3)})) * a_{(2)}^{(2)}\)
\(
sigmoid(z_{(2)}^{(3)}) = a_{(2)}^{(3)}\)
\(
= (a_{(2)}^{(3)} - t_{(2)}^{(3)}) * a_{(2)}^{(3)} * ( 1 - a_{(2)}^{(3)} ) * a_{(2)}^{(2)}\)
\(
\frac {\partial E} {\partial b_{(1)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial b_{(1)}^{(3)}} + \frac {\partial E_{(2)}} {\partial b_{(1)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial a_{(1)}^{(3)}} * \frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} * \frac {\partial z_{(1)}^{(3)}}{\partial b_{(1)}^{(3)}} \)
\(
= \frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(1)}^{(3)} - a_{(1)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(1)}^{(3)}} * \frac { \partial sigmoid (z_{(1)}^{(3)}) } { \partial z_{(1)}^{(3)} } * \frac { \partial ( a_{(1)}^{(2)} w_{(1,1)}^{(3)} + a_{(2)}^{(2)} w_{(1,2)}^{(3)} + b_{(1)}^{(3)} ) } { \partial b_{(1)}^{(3)} } \)
\(
\frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(1)}^{(3)} - a_{(1)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(1)}^{(3)}}
= \frac{1}{2} \cdotp \frac {\partial (t_{(1)}^{(3)})^2 + (a_{(1)}^{(3)})^2 -2 t_{(1)}^{(3)} a_{(1)}^{(3)} } { \partial a_{(1)}^{(3)} }\)
\(
\space \space \space \space = \frac{1}{2} \cdotp (0 + 2*(a_{(1)}^{(3)})^{(2-1)} + -2 t_{(1)}^{(3)}) = a_{(1)}^{(3)} - t_{(1)}^{(3)}\)
\(
\frac { \partial sigmoid (z_{(1)}^{(3)}) } { \partial z_{(1)}^{(3)} } =
sigmoid(z_{(1)}^{(3)}) * (1-sigmoid(z_{(1)}^{(3)}))\)
\(
\frac { \partial ( a_{(1)}^{(2)} w_{(1,1)}^{(3)} + a_{(2)}^{(2)} w_{(1,2)}^{(3)} + b_{(1)}^{(3)} ) } { \partial b_{(1)}^{(3)} }
= 0 + 0 + 1\)
\(
= (a_{(1)}^{(3)} - t_{(1)}^{(3)}) * sigmoid(z_{(1)}^{(3)}) * (1-sigmoid(z_{(1)}^{(3)})) * 1\)
\(
sigmoid(z_{(1)}^{(3)}) = a_{(1)}^{(3)}\)
\(
= (a_{(1)}^{(3)} - t_{(1)}^{(3)}) * a_{(1)}^{(3)} * ( 1 - a_{(1)}^{(3)} ) * 1\)
\(
\frac {\partial E} {\partial b_{(2)}^{(3)}}
= \frac {\partial E_{(1)}} {\partial b_{(2)}^{(3)}} + \frac {\partial E_{(2)}} {\partial b_{(2)}^{(3)}}
= \frac {\partial E_{(2)}} {\partial a_{(2)}^{(3)}} * \frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} * \frac {\partial z_{(2)}^{(3)}}{\partial b_{(2)}^{(3)}} \)
\(
= \frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(2)}^{(3)} - a_{(2)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(2)}^{(3)}} * \frac { \partial sigmoid (z_{(2)}^{(3)}) } { \partial z_{(2)}^{(3)} } * \frac { \partial ( a_{(1)}^{(2)} w_{(2,1)}^{(3)} + a_{(2)}^{(2)} w_{(2,2)}^{(3)} + b_{(2)}^{(3)} ) } { \partial b_{(2)}^{(3)} } \)
\(
\frac {\partial \begin{Bmatrix} \frac{1}{2} (t_{(2)}^{(3)} - a_{(2)}^{(3)})^2 ) \end{Bmatrix} } {\partial a_{(2)}^{(3)}}
= \frac{1}{2} \cdotp \frac {\partial (t_{(2)}^{(3)})^2 + (a_{(2)}^{(3)})^2 -2 t_{(2)}^{(3)} a_{(2)}^{(3)} } { \partial a_{(2)}^{(3)} }\)
\(
\space \space \space \space = \frac{1}{2} \cdotp (0 + 2*(a_{(2)}^{(3)})^{(2-1)} + -2 t_{(2)}^{(3)}) = a_{(2)}^{(3)} - t_{(2)}^{(3)}\)
\(
\frac { \partial sigmoid (z_{(2)}^{(3)}) } { \partial z_{(2)}^{(3)} } =
sigmoid(z_{(2)}^{(3)}) * (1-sigmoid(z_{(2)}^{(3)}))\)
\(
\frac { \partial ( a_{(1)}^{(2)} w_{(2,1)}^{(3)} + a_{(2)}^{(2)} w_{(2,2)}^{(3)} + b_{(2)}^{(3)} ) } { \partial b_{(2)}^{(3)} }
= 0 + 0 + 1\)
\(
= (a_{(2)}^{(3)} - t_{(2)}^{(3)}) * sigmoid(z_{(2)}^{(3)}) * (1-sigmoid(z_{(2)}^{(3)})) * 1\)
\(
sigmoid(z_{(2)}^{(3)}) = a_{(2)}^{(3)}\)
\(
= (a_{(2)}^{(3)} - t_{(2)}^{(3)}) * a_{(2)}^{(3)} * ( 1 - a_{(2)}^{(3)} ) * 1\)
hidden layer 1
...
\(
W^{(2)} = W^{(2)} - \alpha \frac {\partial E}{\partial W^{(2)}} = \frac {\partial E}{\partial W_{(1,1)}^{(2)}} ,
\frac {\partial E}{\partial W_{(2,1)}^{(2)}} ,
\frac {\partial E}{\partial W_{(1,2)}^{(2)}} ,
\frac {\partial E}{\partial W_{(2,2)}^{(2)}} \)
\(
b^{(2)} = b^{(2)} - \alpha \frac {\partial E}{\partial b^{(2)}} =
\frac {\partial E}{\partial b_{(1)}^{(2)}} ,
\frac {\partial E}{\partial b_{(2)}^{(2)}} \)
\(
\frac {\partial E}{\partial W_{(1,1)}^{(2)}} =
\frac {\partial E_{(1)}}{\partial W_{(1,1)}^{(2)}} +
\frac {\partial E_{(2)}}{\partial W_{(1,1)}^{(2)}}\)
\(
=
\frac {\partial E_{(1)}}{\partial a_{(1)}^{(3)}} \times
\frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(3)}}{\partial a_{(1)}^{(2)}} \times
\frac {\partial a_{(1)}^{(2)}}{\partial z_{(1)}^{(2)}} \times
\frac {\partial z_{(1)}^{(2)}}{\partial w_{(1,1)}^{(2)}}\)
\(
+
\frac {\partial E_{(2)}}{\partial a_{(2)}^{(3)}} \times
\frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(3)}}{\partial a_{(1)}^{(2)}} \times
\frac {\partial a_{(1)}^{(2)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(2)}}{\partial w_{(1,1)}^{(2)}} \)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
sigmoid(z_{(1)}^{(3)})
(1-sigmoid(z_{(1)}^{(3)}))
\times
w_{(1,1)}^{(3)}
\times
sigmoid(z_{(1)}^{(2)})
(1-sigmoid(z_{(1)}^{(2)}))
\times
a_{(1)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
sigmoid(z_{(2)}^{(3)})
(1-sigmoid(z_{(2)}^{(3)}))
\times
w_{(2,1)}^{(3)}
\times
sigmoid(z_{(1)}^{(2)})
(1-sigmoid(z_{(1)}^{(2)}))
\times
a_{(1)}^{(1)}
)\)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
a_{(1)}^{(3)}(1-a_{(1)}^{(3)})
\times
w_{(1,1)}^{(3)}
\times
a_{(1)}^{(2)}(1-a_{(1)}^{(2)})
\times
a_{(1)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
a_{(2)}^{(3)}(1-a_{(2)}^{(3)})
\times
w_{(1,1)}^{(3)}
\times
a_{(1)}^{(2)}(1-a_{(1)}^{(2)})
\times
a_{(1)}^{(1)}
)\)
\(
\frac {\partial E}{\partial W_{(2,1)}^{(2)}} =
\frac {\partial E_{(1)}}{\partial W_{(2,1)}^{(2)}} +
\frac {\partial E_{(2)}}{\partial W_{(2,1)}^{(2)}}\)
\(
=
\frac {\partial E_{(1)}}{\partial a_{(1)}^{(3)}} \times
\frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(3)}}{\partial a_{(2)}^{(2)}} \times
\frac {\partial a_{(2)}^{(2)}}{\partial z_{(2)}^{(2)}} \times
\frac {\partial z_{(2)}^{(2)}}{\partial w_{(2,1)}^{(2)}}\)
\(
+
\frac {\partial E_{(2)}}{\partial a_{(2)}^{(3)}} \times
\frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(3)}}{\partial a_{(2)}^{(2)}} \times
\frac {\partial a_{(2)}^{(2)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(2))}}{\partial w_{(2,1)}^{(2)}} \)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
sigmoid(z_{(1)}^{(3)})
(1-sigmoid(z_{(1)}^{(3)}))
\times
w_{(1,2)}^{(3)}
\times
sigmoid(z_{(2)}^{(2)})
(1-sigmoid(z_{(2)}^{(2)}))
\times
a_{(1)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
sigmoid(z_{(2)}^{(3)})
(1-sigmoid(z_{(2)}^{(3)}))
\times
w_{(2,2)}^{(3)}
\times
sigmoid(z_{(2)}^{(2)})
(1-sigmoid(z_{(2)}^{(2)}))
\times
a_{(1)}^{(1)}
)\)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
a_{(1)}^{(3)}(1-a_{(1)}^{(3)})
\times
w_{(1,2)}^{(3)}
\times
a_{(2)}^{(2)}(1-a_{(2)}^{(2)})
\times
a_{(1)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
a_{(2)}^{(3)}(1-a_{(2)}^{(3)})
\times
w_{(2,2)}^{(3)}
\times
a_{(2)}^{(2)}(1-a_{(2)}^{(2)})
\times
a_{(1)}^{(1)}
)\)
\(
\frac {\partial E}{\partial W_{(1,1)}^{(2)}} =
\frac {\partial E_{(1)}}{\partial W_{(1,2)}^{(2)}} +
\frac {\partial E_{(2)}}{\partial W_{(1,2)}^{(2)}}\)
\(
=
\frac {\partial E_{(1)}}{\partial a_{(1)}^{(3)}} \times
\frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(3)}}{\partial a_{(1)}^{(2)}} \times
\frac {\partial a_{(1)}^{(2)}}{\partial z_{(1)}^{(2)}} \times
\frac {\partial z_{(1)}^{(2)}}{\partial w_{(1,2)}^{(2)}}\)
\(
+
\frac {\partial E_{(2)}}{\partial a_{(2)}^{(3)}} \times
\frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(3)}}{\partial a_{(1)}^{(2)}} \times
\frac {\partial a_{(1)}^{(2)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(2))}}{\partial w_{(1,2)}^{(2)}} \)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
sigmoid(z_{(1)}^{(3)})
(1-sigmoid(z_{(1)}^{(3)}))
\times
w_{(1,1)}^{(3)}
\times
sigmoid(z_{(1)}^{(2)})
(1-sigmoid(z_{(1)}^{(2)}))
\times
a_{(2)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
sigmoid(z_{(2)}^{(3)})
(1-sigmoid(z_{(2)}^{(3)}))
\times
w_{(2,1)}^{(3)}
\times
sigmoid(z_{(1)}^{(2)})
(1-sigmoid(z_{(1)}^{(2)}))
\times
a_{(2)}^{(1)}
)\)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
a_{(1)}^{(3)}(1-a_{(1)}^{(3)})
\times
w_{(1,1)}^{(3)}
\times
a_{(1)}^{(2)}(1-a_{(1)}^{(2)})
\times
a_{(2)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
a_{(2)}^{(3)}(1-a_{(2)}^{(3)})
\times
w_{(2,1)}^{(3)}
\times
a_{(1)}^{(2)}(1-a_{(1)}^{(2)})
\times
a_{(2)}^{(1)}
)\)
\(
\frac {\partial E}{\partial W_{(2,2)}^{(2)}} =
\frac {\partial E_{(1)}}{\partial W_{(2,2)}^{(2)}} +
\frac {\partial E_{(2)}}{\partial W_{(2,2)}^{(2)}}\)
\(
=
\frac {\partial E_{(1)}}{\partial a_{(1)}^{(3)}} \times
\frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(3)}}{\partial a_{(2)}^{(2)}} \times
\frac {\partial a_{(2)}^{(2)}}{\partial z_{(2)}^{(2)}} \times
\frac {\partial z_{(2)}^{(2)}}{\partial w_{(2,2)}^{(2)}}\)
\(
+
\frac {\partial E_{(2)}}{\partial a_{(2)}^{(3)}} \times
\frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(3)}}{\partial a_{(2)}^{(2)}} \times
\frac {\partial a_{(2)}^{(2)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(2))}}{\partial w_{(2,2)}^{(2)}} \)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
sigmoid(z_{(1)}^{(3)})
(1-sigmoid(z_{(1)}^{(3)}))
\times
w_{(1,2)}^{(3)}
\times
sigmoid(z_{(2)}^{(2)})
(1-sigmoid(z_{(2)}^{(2)}))
\times
a_{(2)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
sigmoid(z_{(2)}^{(3)})
(1-sigmoid(z_{(2)}^{(3)}))
\times
w_{(2,2)}^{(3)}
\times
sigmoid(z_{(2)}^{(2)})
(1-sigmoid(z_{(2)}^{(2)}))
\times
a_{(2)}^{(1)}
)\)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
a_{(1)}^{(3)}(1-a_{(1)}^{(3)})
\times
w_{(1,2)}^{(3)}
\times
a_{(2)}^{(2)}(1-a_{(2)}^{(2)})
\times
a_{(2)}^{(1)}
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
a_{(2)}^{(3)}(1-a_{(2)}^{(3)})
\times
w_{(2,2)}^{(3)}
\times
a_{(2)}^{(2)}(1-a_{(2)}^{(2)})
\times
a_{(2)}^{(1)}
)\)
\(
\frac {\partial E}{\partial b_{(1)}^{(2)}} =
\frac {\partial E_{(1)}}{\partial b_{(1)}^{(2)}} +
\frac {\partial E_{(2)}}{\partial b_{(1)}^{(2)}}\)
\(
=
\frac {\partial E_{(1)}}{\partial a_{(1)}^{(3)}} \times
\frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(3)}}{\partial a_{(1)}^{(2)}} \times
\frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(2)}} \times
\frac {\partial z_{(1)}^{(2)}}{\partial b_{(1)}^{(2)}}\)
\(
+
\frac {\partial E_{(2)}}{\partial a_{(2)}^{(3)}} \times
\frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(3)}}{\partial a_{(1)}^{(2)}} \times
\frac {\partial a_{(1)}^{(2)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(2))}}{\partial w_{(1)}^{(2)}} \)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
sigmoid(z_{(1)}^{(3)})
(1-sigmoid(z_{(1)}^{(3)}))
\times
w_{(1,1)}^{(3)}
\times
sigmoid(z_{(1)}^{(2)})
(1-sigmoid(z_{(1)}^{(2)}))
\times
1
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
sigmoid(z_{(2)}^{(3)})
(1-sigmoid(z_{(2)}^{(3)}))
\times
w_{(2,1)}^{(3)}
\times
sigmoid(z_{(1)}^{(2)})
(1-sigmoid(z_{(1)}^{(2)}))
\times
1
)\)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
a_{(1)}^{(3)}(1-a_{(1)}^{(3)})
\times
w_{(1,1)}^{(3)}
\times
a_{(1)}^{(2)}(1-a_{(1)}^{(2)})
\times
1
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
a_{(2)}^{(3)}(1-a_{(2)}^{(3)})
\times
w_{(2,1)}^{(3)}
\times
a_{(1)}^{(2)}(1-a_{(1)}^{(2)})
\times
1
)\)
\(
\frac {\partial E}{\partial b_{(2)}^{(2)}} =
\frac {\partial E_{(1)}}{\partial b_{(2)}^{(2)}} +
\frac {\partial E_{(2)}}{\partial b_{(2)}^{(2)}}\)
\(
=
\frac {\partial E_{(1)}}{\partial a_{(1)}^{(3)}} \times
\frac {\partial a_{(1)}^{(3)}}{\partial z_{(1)}^{(3)}} \times
\frac {\partial z_{(1)}^{(3)}}{\partial a_{(2)}^{(2)}} \times
\frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(2)}} \times
\frac {\partial z_{(2)}^{(2)}}{\partial b_{(2)}^{(2)}}\)
\(
+
\frac {\partial E_{(2)}}{\partial a_{(2)}^{(3)}} \times
\frac {\partial a_{(2)}^{(3)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(3)}}{\partial a_{(2)}^{(2)}} \times
\frac {\partial a_{(2)}^{(2)}}{\partial z_{(2)}^{(3)}} \times
\frac {\partial z_{(2)}^{(2))}}{\partial w_{(2)}^{(2)}} \)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
sigmoid(z_{(1)}^{(3)})
(1-sigmoid(z_{(1)}^{(3)}))
\times
w_{(1,3)}^{(3)}
\times
sigmoid(z_{(2)}^{(2)})
(1-sigmoid(z_{(2)}^{(2)}))
\times
1
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
sigmoid(z_{(2)}^{(3)})
(1-sigmoid(z_{(2)}^{(3)}))
\times
w_{(2,2)}^{(3)}
\times
sigmoid(z_{(2)}^{(2)})
(1-sigmoid(z_{(2)}^{(2)}))
\times
1
)\)
\(
=
(
a_{(1)}^{(3)}-
t_{(1)}^{(3)}
\times
a_{(1)}^{(3)}(1-a_{(1)}^{(3)})
\times
w_{(1,2)}^{(3)}
\times
a_{(2)}^{(2)}(1-a_{(2)}^{(2)})
\times
1
)\)
\(
\space \space \space +
(
a_{(2)}^{(3)}-
t_{(2)}^{(3)}
\times
a_{(2)}^{(3)}(1-a_{(2)}^{(3)})
\times
w_{(2,2)}^{(3)}
\times
a_{(2)}^{(2)}(1-a_{(2)}^{(2)})
\times
1
)\)
hidden layer 2
...
\(
\frac {\partial E} {\partial W^{(2)}}
= \begin{bmatrix}
\frac {\partial E}{\partial W_{(1,1)}^{(2)}} &
\frac {\partial E}{\partial W_{(2,1)}^{(2)}} \\
\frac {\partial E}{\partial W_{(1,2)}^{(2)}} &
\frac {\partial E}{\partial W_{(2,2)}^{(2)}} \end{bmatrix}\)
\(
\frac {\partial E}{\partial W_{(1,1)}^{(2)}}\)
\(
= a_{(1)}^{(1)}(a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)})w_{(1,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)})\)
\(
+ a_{(1)}^{(1)}(a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)})w_{(2,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)})\)
\(
\frac {\partial E}{\partial W_{(2,1)}^{(2)}}\)
\(
= a_{(1)}^{(1)}(a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)})w_{(1,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)})\)
\(
+ a_{(1)}^{(1)}(a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)})w_{(2,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)})\)
\(
\frac {\partial E}{\partial W_{(1,2)}^{(2)}}\)
\(
= a_{(2)}^{(1)}(a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)})w_{(1,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)})\)
\(
+ a_{(2)}^{(1)}(a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)})w_{(2,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)})\)
\(
\frac {\partial E}{\partial W_{(2,2)}^{(2)}}\)
\(
= a_{(2)}^{(1)}(a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)})w_{(1,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)})\)
\(
+ a_{(2)}^{(1)}(a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)})w_{(2,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)})\)
\(
= \begin{bmatrix}
a_{(1)}^{(1)} \\
a_{(2)}^{(1)}
\end{bmatrix}\)
\(
\cdotp
\Big(
\begin{bmatrix}
(a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)}) &
(a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)})
\end{bmatrix}\)
\(
\cdotp
\begin{bmatrix}
w_{(1,1)}^{(3)}
&
w_{(1,2)}^{(3)}
\\
w_{(2,1)}^{(3)}
&
w_{(2,2)}^{(3)}
\end{bmatrix}\)
\(
\times
\begin{bmatrix}
a_{(1)}^{(2)}(1-a_{(1)}^{(2)})
&
a_{(2)}^{(2)}(1-a_{(2)}^{(2)})
\end{bmatrix}
\Big)\)
\(
= A1^{T} \cdotp ( (loss\_3 \cdotp W3^{T}) \times (A2 \times (1-A2)) )\)
\( = A1^{T} \cdotp loss\_2 \)
\(
\frac {\partial E} {\partial b^{(2)}}
= \begin{bmatrix}
\frac {\partial E}{\partial b_{(1)}^{(2)}} \\
\frac {\partial E}{\partial b_{(2)}^{(2)}}
\end{bmatrix}\)
\(
= (a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)}w_{(1,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)}\)
\(
+ (a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)}w_{(2,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)}\)
\(
= (a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)}w_{(1,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)}\)
\(
+ (a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)}w_{(2,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)}\)
\(
= (a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)}w_{(1,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)}\)
\(
+ (a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)}w_{(2,1)}^{(3)}a_{(1)}^{(2)}(1-a_{(1)}^{(2)}\)
\(
= (a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)}w_{(1,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)}\)
\(
+ (a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)}w_{(2,2)}^{(3)}a_{(2)}^{(2)}(1-a_{(2)}^{(2)}\)
\(
= (a_{(1)}^{(3)}-t_{(1)}^{(3)})a_{(1)}^{(3)}(1-a_{(1)}^{(3)}\)
\(
\space \space \space
(a_{(2)}^{(3)}-t_{(2)}^{(3)})a_{(2)}^{(3)}(1-a_{(2)}^{(3)})\)
\(
\cdotp
\begin{bmatrix}
W_{(1,1)}^{(3)} &
W_{(1,2)}^{(3)} \\
W_{(2,1)}^{(3)} &
W_{(2,2)}^{(3)}
\end{bmatrix}\)
\(
\times
\begin{bmatrix}
a_{(1)}^{(2)}(1-a_{(1)}{(2)}) \\
a_{(2)}^{(2)}(1-a_{(2)}{(2)})
\end{bmatrix}\)
\(
= ((loss\_3 \cdotp W3^{T}) \times (A2 \times (1-A2)) )\)
\(
= loss\_2\)
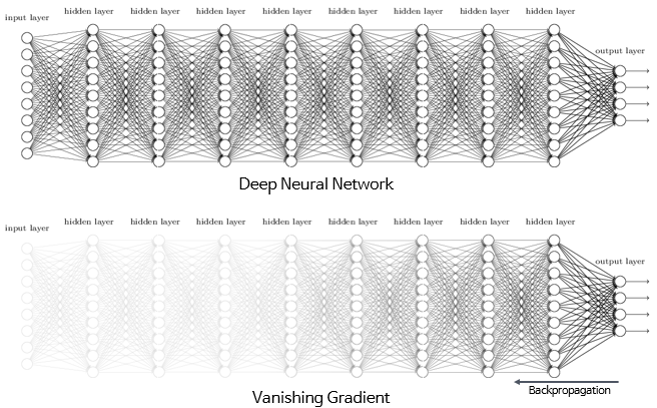
Vanishing Gradient
Sigmoid나 Tanh등 Activation Function의 제한적 실수 범위의 선택으로 Depth가 깊은 Layer에서는 차이가 Squashing되어 소실 되는 특성을 지님
Solution 1 : Relu, Leaky Relu
\( f(x) = max(0,x)\)


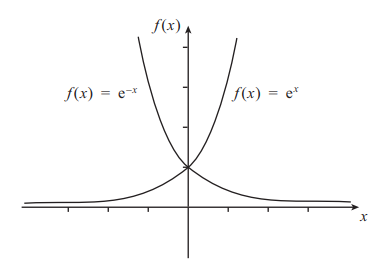
comments powered by Disqus